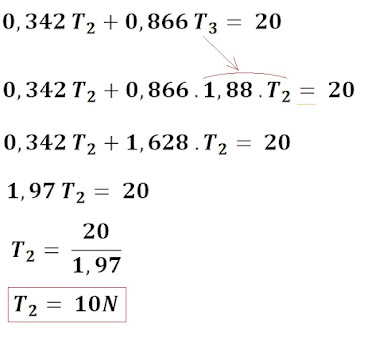Quando um corpo está em repouso, ou seja, não tem nenhum tipo de movimento em relação a um referencial, dizemos que ele está em equilíbrio estático.
Quando um corpo tem dimensões muito pequenas (um corpúsculo), ele pode ser tratado como uma partícula (ou ponto material).
As condições para que uma partícula esteja em equilíbrio estático é que a força resultante sobre ela seja nula, e que esteja em repouso:
- ou, nenhuma força deve atuar sobre a partícula,
- ou, caso forças atuem sobre a partícula, elas devem se cancelar. Ou seja, a soma vetorial deve ser nula.
Por exemplo, imagine uma partícula P sob a ação de três forças, F1, F2 e F3.
Para que essa partícula fique em equilíbrio estático, ela não pode estar em movimento (v = 0), e soma vetorial das três forças deve ser nula:
Vimos que, dependendo das direções dos vetores (e força é um vetor) não é tão simples realizar a soma vetorial.
Em muitas situações, é mais conveniente decompor as forças que atuam sobre uma partícula em suas componentes perpendiculares. Isso facilita bastante a resolução de problemas. Vejamos.
Imagine uma esfera de massa m suspensa por um fio (1), que por sua vez está preso aos fios 2 e 3, como mostra a figura abaixo:
O nó P entre os fios 1, 2 e 3 pode ser considerado como um ponto material. E, este ponto está sob a ação de três forças, as trações T1, T2 e T3 transmitidas pelos fios.
Isolando o nó, teremos:
Decompondo as trações T1 e T2 nas direções horizontal (x) e vertical (y), teremos:
Quando decompomos uma força, é equivalente a trocá-la por duas forças perpendiculares equivalentes a ela. Sendo assim, depois da decomposição, é como se somente tivéssemos forças em direções perpendiculares:
Para que a partícula esteja em equilíbrio, as forças que têm a mesma direção devem se cancelar. Sendo assim, em determinada direção, a soma dos módulos das forças em certo sentido deve ser igual à soma dos módulos das forças no sentido oposto:
Desse modo, teríamos:
Na horizontal (x):
Na vertical (y):
O que nos dá o seguinte sistema de equações:
Observe, que cada direção nos dá uma equação.
Agora, usando as definições de seno, cosseno e tangente no triângulo retângulo, precisamos colocar as componentes em função das trações.
Vamos relembrar essas definições trigonométricas?
O um triângulo retângulo abaixo têm dois catetos (C e C'), e a hipotenusa (H). Além do ângulo reto (90ᵒ), tem também dois ângulos agudos, α e β:
Por definição, o seno do ângulo escolhido (α ou β), é:
O cosseno, é:
E, a tangente:
Assim, para o ângulo α, teríamos:
Para o ângulo β, teríamos:
Como exemplo concreto, dado o triângulo retângulo abaixo:
Temos:
Agora vamos voltar ao exemplo 1. Precisamos colocar no sistema de equações que foi obtido, as compontes das trações em função das trações. Vamos começar por T2:
Em relação ao ângulo de 20ᵒ no triângulo retângulo de cima, T2y é o cateto oposto, sendo assim:
No triângulo retângulo de baixo, T2x é o cateto adjacente (vizinho) ao ângulo de 20ᵒ, sendo assim:
Para a tração T3:
Em relação ao ângulo de 60ᵒ no triângulo retângulo de cima, T3y é o cateto oposto, sendo assim:
No triângulo retângulo de baixo, T3x é o cateto adjacente (vizinho) ao ângulo de 60ᵒ, sendo assim:
Agora, no sistema de equações só aparecem as próprias trações, e não as suas componentes. Se, uma das das trações for conhecida, podemos encontrar os valores das outras duas.
Agora vamos transformar o que vimos em um problema.
Exemplo
Uma esfera de massa m=2,0kg está suspensa por um fio (1), que por sua vez está preso aos fios 2 e 3, como mostra a figura abaixo:
a) Qual o módulo da tração no fio 2?
b) Qual a tração no fio 3?
Resolução:
A esfera está em equilíbrio estático. Logo, as forças que atuam sobre ela se cancelam. Então P=T1. Como P=20N, T1=20N.
Desse modo, o sistema de equações que obtemos anteriormente, fica:
O método de resolução do sistema você escolhe. Vamos usar o método da substituição.
A primeira equação, nos dá:
Substituímos esse resultado na segunda equação, obtemos:
Substituindo agora o valor de T2 encontrado na primeira equação, obtemos:
Respostas
a) 10N
b) 19N
Obs.: Como a massa tem dois algarismos significativos, as trações também têm dois algarismos significativos.
Corpo Extenso
Um corpo extenso é aquele que tem dimensões consideráveis.
Quando uma força atua sobre uma partícula, o único efeito que pode produzir é a translação (deslocamento em certa direção):
Mas quando uma força atua sobre um corpo extenso, pode provocar tanto a translação,
Veremos melhor este efeito (rotação) em outro momento.
Mas em problemas em que as forças não possam provocar rotações, só precisamos nos preocupar com a força resultante nula, como fizemos no caso das partículas.
Vamos ver alguns exemplos sobre Estática em que não precisamos nos preocupar com o efeito de rotação das forças? Clique no link abaixo para avançar.